832. Increasing
subsequence
Given n integers x1, x2, ..., xn. Delete from them the least number of integers so
that the rest were in ascending order.
Input. The first line contains the number n (1 ≤ n ≤ 105).
The second line contains the integers x1, x2, ..., xn (1 ≤ xi ≤
60 000).
Output. Print in the first line the number
of not erased integers. In the second line print the list of unerased integers
in the original order. If several answers exist, print any.
|
Sample
input |
Sample
output |
|
6 2 5 3 4 6 1 |
4 2 3 4 6 |
SOLUTION
longest increasing
subsequence
Algorithm analysis
The largest increasing subsequence must be found and printed.
For each element xi (1 ≤ i ≤ n), find the length of the LIS that
ends at xi. Store these values in array L. This information is enough to find the LIS
itself in linear time. The length of the LIS equals to the
maximum number k in array L. Let this largest
number k be in the index pos.
Then the LIS ends with the number xpos. Decrease pos
until L[pos] becomes equal to k – 1. The current xpos will be the penultimate element in the LIS. And
so on, we continue to move the pos index to the start of
array L, stopping at the first positions for which L[pos] = k – 2, …, L[pos] =
0.
Theorem. Consider the indices i1 < i2 < …< im,
for which L[i1] = L[i2] = …= L[im]. Then the sequence xi1, xi2, …, xim is decreasing.
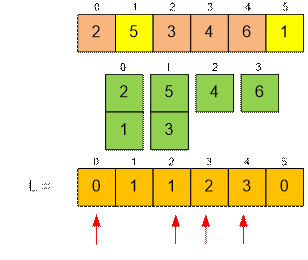
Example
The solitaire layout looks like:
L[i] contains the
number of the pile where the card xi will be placed (the piles
are numbered starting from zero).
Algorithm realization
Declare the arrays.
#define MAX 60001
int x[MAX], lis[MAX], L[MAX];
Print the LIS.
void PrintSeq(int
pos)
{
if (size <
0) return;
while(L[pos]
!= size) pos--;
size--; PrintSeq(pos-1);
printf("%d
",x[pos]);
}
The main part of the program. Read the input sequence.
scanf("%d",&n);
for(i = 0; i < n; i++)
scanf("%d",&x[i]);
Fill the arrays.
for (len = i = 0; i < n; i++)
{
pos = lower_bound(lis,lis+len,x[i]) - lis;
lis[pos] = x[i];
L[i] = pos;
if (pos ==
len) len++;
}
Print the largest increasing subsequence.
printf("%d\n",len); size = len - 1;
PrintSeq(n-1);
printf("\n");